Strange as it may sound, the power of mathematics rests on its evasion of all unnecessary thought and on its
wonderful saving of mental operations.
Ernst Mach
Welcome to Math1089 – Mathematics for All!
I’m genuinely grateful that you’ve taken time from your busy schedule to stop by. This space is all about celebrating the elegance and fascination of mathematics. While math is indeed a beautiful subject, I understand it doesn’t always feel that way—especially for students who haven’t yet discovered the joy in numbers and patterns. My hope is to help change that, one insight at a time.
Thank you for visiting Math1089! I truly appreciate you taking the time out of your busy day to explore this space dedicated to the beauty and wonder of mathematics. Math is a beautiful subject, but I understand it’s not always easy to see that beauty right away—especially for students who may not yet share a passion for numbers and patterns.
In this blog post, we are going to dive into the fascinating world of magic squares, but with an exciting twist! Instead of using a regular set of numbers, we will construct a magic square of order four using only numbers formed from the digits 0, 2, and 5.
That’s right—every number in the square will be made up exclusively of these three digits. What makes this magic square even more captivating is that one of the entries in the square is the number 2025 and 2520—a number with a neat symmetry and significance, especially for number enthusiasts. Our goal will be to examine this magic square in depth:
Stay tuned as we analyze the square’s rows, columns, and diagonals to uncover the underlying mathematical beauty and symmetry.
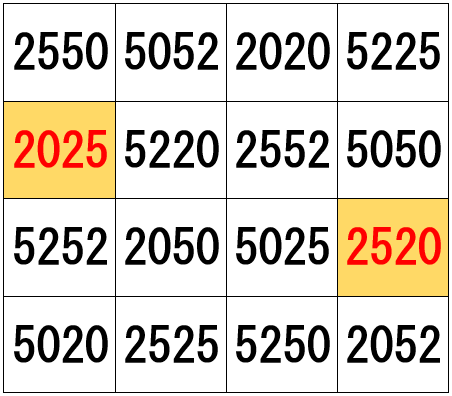
Few Notable Properties
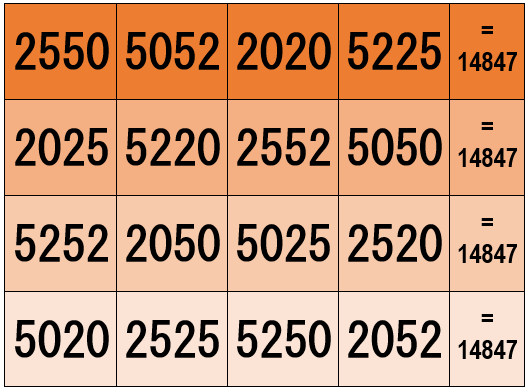
(a) The sum of the row elements in each row is equal to 14847. For example,
2520 + 5052 + 2020 + 5225 = 14847
2025 + 5220 + 2552 + 5050 = 14847
5252 + 2050 + 5025 + 2520 = 14847
5020 + 2525 + 5250 + 2052 = 14847
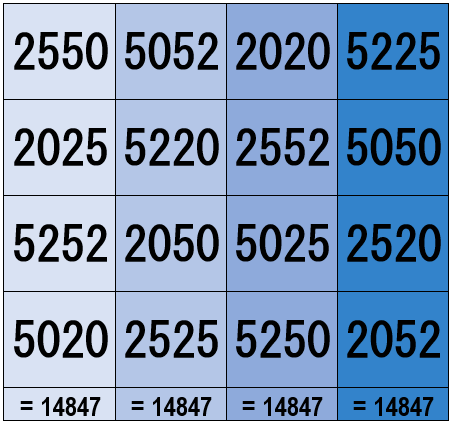
(b) The sum of the column elements in each column is equal to 14847. For example,
2550 + 2025 + 5252 + 5020 = 14847
5052 + 5220 + 2050 + 2525 = 14847
2020 + 2552 + 5025 + 5250 = 14847
5225 + 5050 + 2520 + 2052 = 14847
(c) The sum of the diagonal elements is also equal to 14847. For example,
5225 + 2552 + 2050 + 5020 = 14847 (green)
2550 + 5220 + 5025 + 2052 = 14847 (light blue)

(d) The sum of the corner elements is also equal to 14847. For example,
2550 + 5225 + 2052 + 5020 = 14847

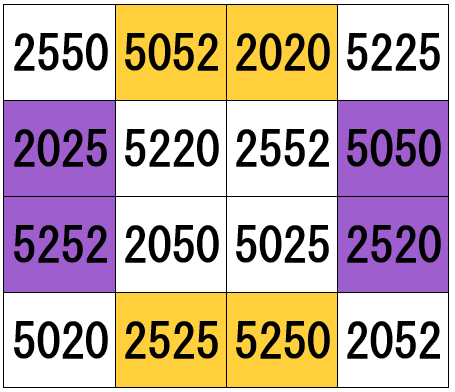
(e) The sums of the numbers in the two sets of like coloured cells are again the same number 14847. For example,
5052 + 2020 + 5250 + 2525 = 14847 (gold)
2025 + 5252 + 2520 + 5050 = 14847 (purple)
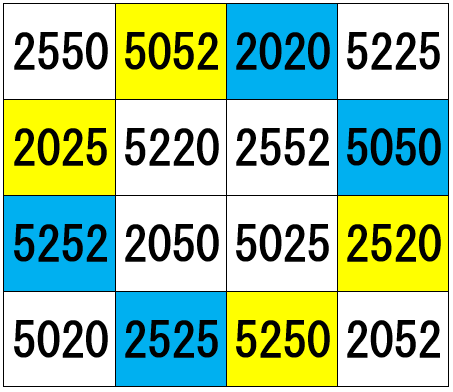
(f) The sums of the numbers in the two sets of like coloured cells are again the same number 14847. For example,
5052 + 2520 + 5250 + 2025 = 14847 (yellow)
5252 + 2525 + 5050 + 2020 = 14847 (blue)
(g) The sum of the numbers in the four central cells is again 14847. For example,
5220 + 2552 + 5025 + 2050 = 14847

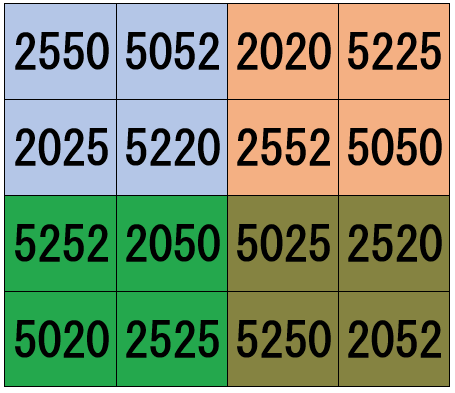
(h) The sums of the numbers in the like-coloured 2 × 2 blocks are all 14847. For example,
2550 + 5052 + 5220 + 2025 = 14847 (light blue)
2020 + 5225 + 5050 + 2552 = 14847 (orange)
5025 + 2520 + 2052 + 5250 = 14847 (olive green)
5252 + 2050 + 2525 + 5020 = 14847 (green)
(i) The sums of the numbers in the like-coloured 2 × 2 blocks are also 14847. For example,
2025 + 5220 + 2050 + 5252 = 14847 (gray)
2552 + 5050 + 2520 + 5025 = 14847 (lime)

This blog is as much yours as it is mine. Would you like to contribute an exceptional, non-routine article and have it published on Math1089? Perhaps you have a preliminary idea that you wish to see in its published form—please share your ideas by dropping us a line.
We wholeheartedly welcome your contributions and eagerly anticipate featuring your ideas on “Math1089 – Mathematics for All” in our next captivating mathematics blog post. Thank you for being a part of our journey, and we look forward to your involvement in shaping the future content of Math1089. See you soon for another intriguing exploration into the world of mathematics!